Der vorletzte der angekündigten Artikel aus meinem Studium befasst sich mit Dithering, hier speziell zur Anwendung als Web-/OpenGL-Shader. Ich habe allerdings aus Zeitgründen keine Implementierung abgeliefert, sondern lediglich einen Ansatz, wie die Implementierung umgesetzt werden könnte.
Beschreibung des grafischen Ditherings mit Implementierungsansatz
Miron Schmidt 2023
1. Grundlagen
Dithering ist die Anwendung von Rauschen zur Verteilung von Quantisierungsfehlern.1 In der Computergrafik dient Dithering oft der Darstellung von Bildern in begrenzten Farbpaletten, etwa, um Bitplanes und damit Speicher oder Rechenzeit einzusparen (auch Farbreduktion genannt).
Der Begriff „Rauschen“ ist hier missverständlich, da nicht unbedingt eine zufällige Verteilung gemeint ist (siehe allerdings Abschnitt 2), sondern oft regelmäßige Rastermuster. Für die Anordnung gibt es zahlreiche Algorithmen, z. B. Ordered Dithering2 , Floyd-Steinberg3 oder Burkes4 .
Grundsätzlich werden bei der Farbreduktion Schwellenwerte gebildet, nach denen aus einer Farbe die nächstmögliche im vorhandenen Farbpool errechnet wird. Im einfachsten Fall, der Darstellung mit einem Bit, kann die Farbe im Pool 0 oder 1 sein. Alle Farbwerte mit einem Durchschnittswert über 50 % erhalten dann den Wert 1, die anderen den Wert 0. Beim Dithering geschieht dies weiterhin, der Schwellenwert für jedes Pixel wird aber verändert, um eine weniger harte Abstufung zu erreichen.
2. Beschreibung
Die einfachste Form des Dithering ist sehr wohl die Überlagerung von Rauschen auf das Bild (Abb. 1c). Der Schwellenwert wird dadurch um einen Zufallsfaktor verändert, sodass die Pixel stärker gestreut werden.
Bei den meisten Dithering-Algorithmen werden jedoch die Folgepixel mit dem Quantisierungsfehler des aktuellen Pixels verrechnet.
Einer der bekanntesten und ältesten Dithering-Algorithmen ist der nach Floyd und Steinberg5 , den ich hier exemplarisch vorstellen möchte.


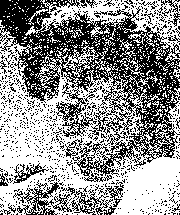

Hierbei wird der Quantisierungsfehler durch 16 geteilt und auf die Schwellenwerte für umliegende Pixel verteilt: 7 Anteile auf das horizontal folgende Pixel, 3 auf das links unter dem Pixel liegende Pixel, 5 auf das direkt darunter liegende und 1 auf das rechts unter ihm liegende. Die bereits verarbeiteten Pixel werden also nicht mehr verändert, Pixel in der nächsten Zeile dafür möglicherweise später noch einmal. Durch diese Verteilung wird die Wahrscheinlichkeit verändert, dass Pixel den Schwellenwert erreichen, und es entsteht das in Abbildung 1d dargestellte Muster.
3. Implementierungsansatz
Der folgende Pseudocode6 gibt den Floyd-Steinberg-Algorithmus wieder:
for each y from top to bottom do
for each x from left to right do
oldpixel := pixels[x][y]
newpixel := find_closest_palette_color(oldpixel)
pixels[x][y] := newpixel
quant_error := oldpixel - newpixel
pixels[x + 1][y ] := pixels[x + 1][y ]
+ quant_error * 7 / 16
pixels[x - 1][y + 1] := pixels[x - 1][y + 1]
+ quant_error * 3 / 16
pixels[x ][y + 1] := pixels[x ][y + 1]
+ quant_error * 5 / 16
pixels[x + 1][y + 1] := pixels[x + 1][y + 1]
+ quant_error * 1 / 16Um Floyd-Steinberg-Dithering in einem Shader etwa in WebGL zu implementieren, würde dieser Code im Multipassverfahren angewendet werden: Zuerst wird das Bild der Szene in ein dafür angelegtes Framebuffer-Objekt gerendert, dann wird auf dieses Framebuffer-Objekt in einem zweiten Pass der Dithering-Algorithmus angewendet (z. B. nach Reduktion der Bitplanes) und wiederum in den Standard-Framebuffer gerendert, normalerweise also auf dem Bildschirm ausgegeben.
- vgl. die Masterarbeit von Larence G. Roberts, in abgewandelter Artikelform unter http://www.packet.cc/files/pic-code-noise.html (archiviert im Internet Archive, Stand: 6.2.2024) ↩︎
- s. etwa https://en.wikipedia.org/wiki/Ordered_dithering (Stand: 6.2.2024) ↩︎
- s. etwa https://en.wikipedia.org/wiki/Floyd-Steinberg_dithering (Stand: 6.2.2024) ↩︎
- eine Weiterentwicklung der Matrix von Jarvis, Judice und Ninke, beschrieben z. B. unter https://tannerhelland.com/2012/12/28/dithering-eleven-algorithms-source-code.html ↩︎
- vgl. den Wikipedia-Artikel zum Floyd-Steinberg-Algorithmus (Stand: 10.2.2024) ↩︎
- s. ebd. ↩︎

